Background:

Inference (prediction) is believed to be a fundamentally important computational function for biological sensory systems. For example, the Bayesian model of sensory (e.g., visual) signal processing postulates that the cortical networks in the brain encode a probabilistic belief about reality. The belief state (modeled as a posterior distribution in the Bayes; formalism) is updated based on a comparison between the novel stimuli (from senses) and the internal prediction.

Objective:

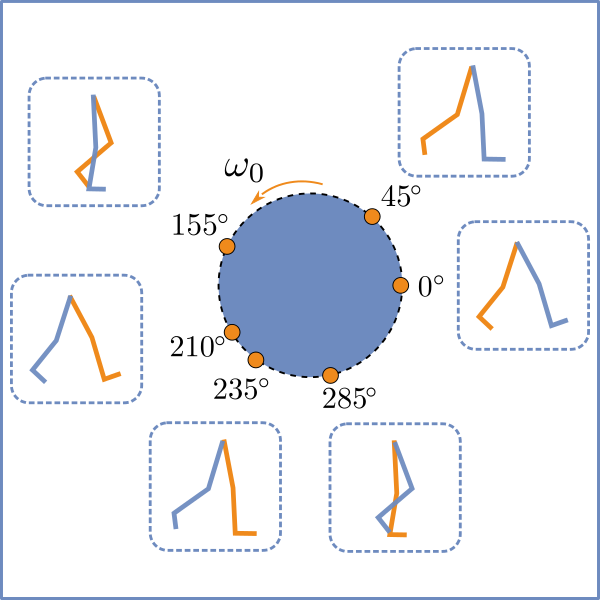A natural question to ask then is whether there is a rigorous methodology (and algorithms) to implement complex forms of prediction (via Bayes theorem) at the level of neurons - the computing elements of the brain. The goal of our research is to develop neuromorphic architectures for implementing Bayes rule. One such architecture is the coupled oscillator feedback particle filter model. A single oscillator is a simplified model of a single spiking neuron, and the coupled oscillator model represents a neuronal network.

Background:

Nonlinear estimation algorithms are a widely pervasive platform technology. One specific application domain is target state estimation (target tracking). It is important in a number of Intelligence, Surveillance, and Reconnaissance (ISR) systems and products: Radar-based air moving target indicator (AMTI) systems are used in surveillance of enemy aircraft. In missile defense, the objective is to track and intercept ballistic objects, including parts of aging satellites that may re-enter the atmosphere. The radar-based ground moving target indicator (GMTI) systems are used for military surveillance and increasingly for counter-terrorism applications. In wide-area maritime surveillance, an airborne aircraft uses radar-based measurements to detect and track maritime surface vessels. In related applications, passive sonar devices are employed for the purposes of underwater submarine tracking. Apart from these, such algorithms also find extensive use in civilian applications, including air traffic surveillance, weather surveillance, ground mapping, geophysical surveys, remote sensing, autonomous navigation, and robotics. For example, current air traffic surveillance systems use radar-based measurements to track aircraft.

State-of-the-art and its limitations:

Current state estimation systems use a Kalman filter, or one of its extensions (e.g., extended Kalman filter). The limitations of these tools in applications arise on account of nonlinearities in signal and sensor models. The nonlinearities lead to a non-Gaussian multi-modal conditional distribution. For such cases, Kalman and extended Kalman filters are known to perform poorly.

Feedback Particle Filter:

A feedback particle filter is a novel algorithm for nonlinear estimation that has been developed by our research group. The feedback particle filter provides for a generalization of the Kalman filter to a general class of nonlinear non-Gaussian problems. Our algorithm inherits many of the structural features, such as an innovation error-based feedback structure and robustness properties, which have made the Kalman filter so widely applicable over the past five decades. Compared to other types of particle filter algorithms, our algorithm provides more accurate estimates at a fraction of the computational cost. Our algorithms are also more robust, cost-effective, and relatively easier to debug and implement. This is now being documented in open literature, both in research carried out in our group as well as externally by independent groups.

Background:

In engineering applications, emergent collective behavior is almost always viewed as a bane. Take, for example, the scenes witnessed at the opening of London's Millennium bridge.

On June 10, 2000, a bridge opened in London to mark the dawn of the new millennium. As people poured on to the Millennium bridge, it quickly became apparent that there was a problem. In the words of Pat Dallard of Arup Corporation, the firm responsible for bridge design, ''We were witnessing the bridge performing in a way that we hadn't anticipated ... We felt that we understood it very well and here it is doing something completely unexpected.''

The "something unexpected" referred to in Dallard's interview can be viewed on the YouTube video.

The roots of the problem lay in the assumptions made in the design of the bridge. It is commonly assumed that the motion of pedestrians is incoherent. On this particular day, on this particular bridge, Pat Dallard observed that the ''motion of the crowd was synchronized with the motion of the bridge.''

As can be seen in the video, as the bridge began to sway, the pedestrians modified their gait to maintain balance. The emergence of coherence created a lateral force on the bridge that reinforced its sway. It is this positive feedback that led to the striking oscillatory motion of the bridge that could have resulted in its collapse.

In the case of a bridge, there is no question that the emergent dynamic behavior in the form of the synchronized motion of the crowd is undesirable. We come to the same conclusion in many other contexts: For example, the power grid can show similar cascading oscillations, with similar consequences.

Objective:

The objective here is to explore phase transition and self-organization in large population dynamic systems. A central goal of this research is the largely classical question of emergent behavior in these dynamical systems:

How does collective (global) behavior depend upon the local interactions?

We bring new tools to this and surrounding questions, along with new applications in engineering and biology.

Motivation:

A source of inspiration for our research is the optimistic view taken in other fields, such as biology and economics.

A premise of our research is that in biological and economic systems, the emergent collective behavior is at the very core of what makes the system useful and interesting. In economics, for example, Adam Smith's invisible hand guides the smooth functioning of the free markets. Even though an individual merely seeks her own selfish gain, the invisible hand promotes the greater collective good. The invisible hand can be viewed as a self-organized collective state that emerges within a large population of self-interested individuals.

The invisible hand may well be present in the functioning of biological systems too. For instance, neural rhythms in brain circuits (e.g., the thalamocortical circuit) have been linked to information processing, communication, neuronal plasticity, memory formation, and ultimately consciousness itself.1 The self-generated (emergent) neural rhythms can be viewed as an invisible hand that guides the smooth functioning of a healthy brain. The analogy is meant to be suggestive – the invisible hand represents the collective network behavior that promotes an end greater than the activity of an individual neuron.

As the example of the Millennium bridge suggests, the collective emergent behavior need not always be desirable – the invisible hand can sometimes turn into a fist: In financial markets, liquidity can freeze up as a result of the self-reinforcing lock-step behavior of the individuals. In a recent article in The New Yorker magazine, John Cassidy makes a powerful analogy between synchronized crowd behavior in the millennium bridge and the credit-freeze experienced in the recent financial crisis. In biology, certain forms of thalamocortical neural rhythms are a symptom of neuropathological disorder such as epilepsy.

Research Theme:

There are many approaches within the field of economics to understand the relationship between individual and collective (group) behavior. Prominent among these is the application of game theory to obtain economic equilibria based on rational actions of self-interested individuals. These equilibria may not be ideal: Even when the behavior of individuals is entirely rational from the individual's perspective, the resulting collective behavior in the marketplace may be catastrophic. The bridge provides another case in which the synchronized motion of crowd can be viewed as an example of such ''rational irrationality.'' Any individual pedestrian will naturally modify their gait as a rational strategy to avoid falling down on a swaying bridge. However, this innocent behavior of individuals collectively sustains and reinforces the (irrational) swaying of the bridge.

In the field of dynamical systems, the emergent collective behavior in large population systems is regarded as a phase transition. In the Millenium bridge, the change of mode from a quiescent bridge to one exhibiting violent oscillation is an example of the phase transition.

The game-theoretic viewpoint is central to our study of emergent dynamics in large population dynamic systems. The phase transition in the Millennium bridge represents a particularly simple example that nonetheless captures all the main features: a collection of heterogeneous nonlinear systems (pedestrians) with selfish goals (of crossing the bridge while maintaining balance), that exhibits a phase transition from an equilibrium state (where pedestrian motion is incoherent) to a non-equilibrium state (where the pedestrian motion is synchronized). The non-equilibrium state represents an emergent dynamic behavior of the collective that sustains and reinforces the swaying of the bridge, that is not the intent of the pedestrians' actions.

Results:

We have developed a methodological framework, rooted in dynamical systems theory and game theory, that relates the emergent collective dynamic behavior of the population to the underlying interaction/control mechanisms -- in particular those resulting from competitive interactions amongst individuals.